Advertisements
Advertisements
प्रश्न
An aeroplane, at an altitude of 250 m, observes the angles of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. If the boats are on the opposite sides of the aeroplane, find the width of the river. Write the answer correct to the nearest whole number.
उत्तर
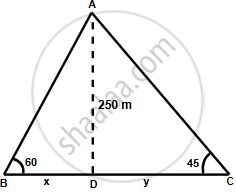
Let A be the position of the airplane and let BC be the river. Let D be the point in BC just below the airplane.
B and C be two boats on the opposite banks of the river with angles of depression 60° and 45° from A.
In ΔADC,
`tan 45^circ = (AD)/(DC)`
`=> 1 = 250/y`
`=>` y = 250 m = DC
In ΔADB,
`tan 60^circ = (AD)/(BD)`
`=> sqrt(3) = 250/x`
`=> x = 250/sqrt(3)`
= `(250sqrt(3))/3`
= `(250 xx 1.732)/3`
= 144.3 m = BD
∴ BC = BD + DC
= 144.3 + 250
= 394.3 ≈ 394 m
Thus, the width of the river is 394 m.
APPEARS IN
संबंधित प्रश्न
Evaluate without using trigonometric tables.
`2((tan 35^@)/(cot 55^@))^2 + ((cot 55^@)/(tan 35^@)) - 3((sec 40^@)/(cosec 50^@))`
A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45°, (ii) 60°. Find the height of the tower in each case.
A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on the opposite bank is 60°. When he moves 40 m away from the bank, he finds the angle of elevation to be 30°. Find:
- the height of the tree, correct to 2 decimal places,
- the width of the river.
Find AD.

A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
In figures, find the length CF.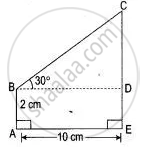
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
Two-person standing on the same side of a tower in a straight line with it measures the angle of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m find the distance between the two-person.
A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff. At a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff are 54° and 42° respectively. Find the height of the flagstaff. Give your answer correct to nearest metre.

