Advertisements
Advertisements
प्रश्न
A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
उत्तर
Let the height of the tower be ‘h’ m.
In Δ ADC , tan 45° = `h/(20 + x)`
1 = `h /(20+ x`
⇒ h = 20 + x
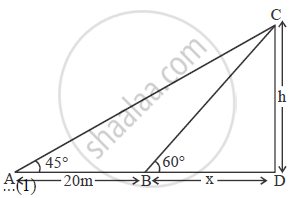
Also , In ΔBDC , tan 60° = `h/x`
`sqrt(3) = h / x`
⇒ x = `h/(sqrt(3))` ...(2)
h = 20 + `h/sqrt(3)`
`h - h/sqrt(3) = 20`
`h((sqrt(3) -1)/sqrt(3)) = 20`
`h = (20 sqrt(3)) /((sqrt(3) - 1)) xx ((sqrt(3) + 1)) /(( sqrt(3) +1 )`
`= (20 (3 + sqrt(3)))/(3-1)`
`= (20 (3+1.732))/2`
= 10 (4.732)
Height of the tower . h = 47.32 m
APPEARS IN
संबंधित प्रश्न
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
Find AD.

A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
An observer point for ships moving in the sea 500m above the sea level. The person manning this point observes the angle of depression of twc boats as 45° and 30°. Find the distance between the boats when they are on the same side of the observation point and when they are on opposite sides of the observation point.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
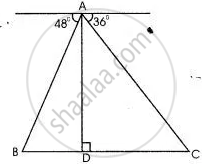
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
A man on the deck of a ship is 10 m above water level. He observes that the angle of elevation of the top of a cliff is 42° and the angle of depression of the base is 20°. Calculate the distance of the cliff from the ship and the height of the cliff.
