Advertisements
Advertisements
प्रश्न
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
उत्तर
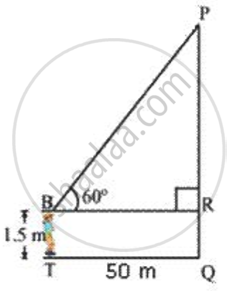
Let the position of the boy be at point T.
BR = TQ = 50 m
RQ = BT= 1.5 m
In ΔPRB
`"PR"/"BR" = tan 60^circ`
`"PR"/50 = sqrt(3)`
`"PR" = 50sqrt(3)`
Height of the tower
`= "PQ" = "PR + RQ" = 50sqrt(3) + 1.5 = 50 xx 1.732 + 1.5 = 86.6 + 1.5 = 88.1 "m"`
Thus , the height of the tower is approximately 88 m.
APPEARS IN
संबंधित प्रश्न
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east, are found to be 30° and 45° respectively. Find the distances of the two stones from the foot of the hill.
Calculate BC.
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
A boy is 1.54 m tall. Standing at a distance of 3m in front of a 4.54 m high wall he can just manage to see the sun. Find the angle of elevation of the sun.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
From a point 10 m above the ground , the angle of elevation of the top of a tower is α and the angle of depression is β . If tan α = `5/2` and tan β = `1/4` , calculate the height of the tower to the nearest metre .
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
Vertical tower is 20m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
