Advertisements
Advertisements
प्रश्न
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
उत्तर
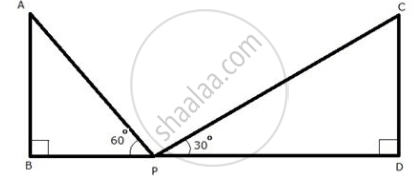
Let AB and CD be the two towers of height h m.
Let P be a point in the roadway BD such that BD = 150 m, ∠APB = 60° and ∠CPD = 30°
In ΔABP,
`(AB)/(BP) = tan 60^circ`
`=> BP = h/(tan 60^circ) = h/sqrt(3)`
In ΔCDP,
`(CD)/(DP) = tan 30^circ`
`=> PD = 1/sqrt(3)`
Now, 150 = BP + PD
`=> 150 = h/sqrt(3) + 1/sqrt(3)`
∴ `h = 150/(sqrt(3) + 1/sqrt 3)`
= `150/2.309`
= 64.95 m
Hence, height of the pillars is 64.95 m.
The point is `(BP)/sqrt(3)` from the first pillar.
That is the position of the point is `64.95/sqrt(3) m` from the first pillar.
The position of the point is 37.5 m from the first pillar.
APPEARS IN
संबंधित प्रश्न
Evaluate without using trigonometric tables.
`2((tan 35^@)/(cot 55^@))^2 + ((cot 55^@)/(tan 35^@)) - 3((sec 40^@)/(cosec 50^@))`
A man observes the angle of elevation of the top of a building to be 30o. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60o. Find the height of the building correct to the nearest metre.
The angle of elevation of the top of an unfinished tower from a point at a distance of 80 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
Calculate AB.

A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60°. When he moves 50 m away from the bank, he finds the angle of elevation to be 30°.
Calculate :
- the width of the river;
- the height of the tree.
The angles of depression and elevation of the top of a 12m high building from the top and the bottom of a tower are 60° and 30° respectively. Find the height of the tower, and its distance from the building.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° from two observing points 100 m apart to his right. Find the height from which he falls and the distance of the point where he falls on the ground from the nearest observation pcint.
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
From a lighthouse, the angles of depression of two ships on opposite sides of the lighthouse were observed to be 30° and 45°. If the height of the lighthouse is 90 metres and the line joining the two ships passes through the foot of the lighthouse, find the distance between the two ships, correct to two decimal places.
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
