Advertisements
Advertisements
प्रश्न
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
उत्तर
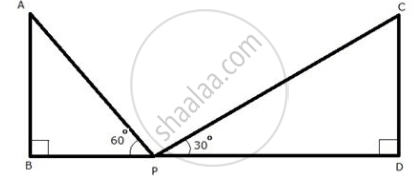
Let AB and CD be the two towers of height h m.
Let P be a point in the roadway BD such that BD = 150 m, ∠APB = 60° and ∠CPD = 30°
In ΔABP,
`(AB)/(BP) = tan 60^circ`
`=> BP = h/(tan 60^circ) = h/sqrt(3)`
In ΔCDP,
`(CD)/(DP) = tan 30^circ`
`=> PD = 1/sqrt(3)`
Now, 150 = BP + PD
`=> 150 = h/sqrt(3) + 1/sqrt(3)`
∴ `h = 150/(sqrt(3) + 1/sqrt 3)`
= `150/2.309`
= 64.95 m
Hence, height of the pillars is 64.95 m.
The point is `(BP)/sqrt(3)` from the first pillar.
That is the position of the point is `64.95/sqrt(3) m` from the first pillar.
The position of the point is 37.5 m from the first pillar.
APPEARS IN
संबंधित प्रश्न
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30° with the ground.
Calculate AB.

From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
The horizontal distance between two trees of different heights is 100m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 150m, find the height of the first tree.
Two boats approaching a light house in mid sea from opposite directions observe the angle of elevation of the top of the light house as 30° and 45° respectively. If the distance between the two boats is 150m, find the height of the light house.
From the top of a light house 96m high, the angles of depression of two ships in the river and at the same level as the base of the light house and on the same side of it, are α and β. If tan α = `1/4` and tan β = `1/7`, find the distance between the ships.
The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
A man on the top of a tower observes a truck at an angle of depression ∝ where `∝ = 1/sqrt(5)` and sees that it is moving towards the base of the tower. Ten minutes later, the angle of depression of the truck is found to `β = sqrt(5)`. Assuming that the truck moves at a uniform speed, determine how much more ti me it will take to each the base of the tower?
A man on the top of vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower? (Give your answer correct to nearest seconds).
