Advertisements
Advertisements
प्रश्न
The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
उत्तर
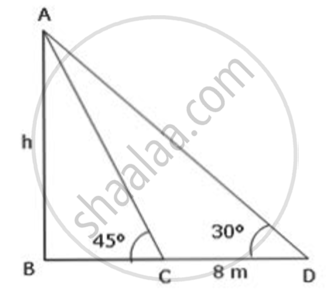
Let the height of the statue (AB) be h.
In ΔABC,
`tan45^circ = "AB"/"BC"`
⇒ BC = h
In ΔABD,
`tan30^circ = "AB"/"BD"`
`1/sqrt(3) = "AB"/("BC + CD")`
h + 8 = `sqrt(3)`h (∵ BC = h)
⇒ `"h"(sqrt(3)` - 1) = 8
⇒ h = `8/(sqrt(3) - 1) × (sqrt(3) + 1)/(sqrt(3) + 1)`
⇒ h = `(8(sqrt(3) + 1))/2 = 4(sqrt(3) + 1) = 4 xx 2.732 = 10.928 ≈ 10.93`
Thus, the height of the tower is 10. 93 m.
APPEARS IN
संबंधित प्रश्न
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. What was the height of the tree before it was broken?
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°; find the uniform speed of the aeroplane in km per hour.
A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
Due to a heavy storm, a part of a banyan tree broke without separating from the main. The top of the tree touched the ground 15 m from the base making an angle of 45° with the ground. Calculate the height of the tree before it was broken.
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
