Advertisements
Advertisements
प्रश्न
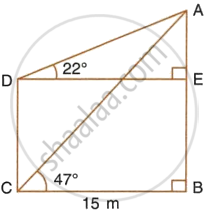
From the figure, given below, calculate the length of CD.
उत्तर
In right ΔACB, we have
`tan theta = (AB)/(BC)`
`\implies tan 47^circ = (AB)/15`
`\implies 1.0724 = (AB)/15`
∴ AB = 1.0724 × 15
= 16.0860 m
= 16.09 m.
And in right ΔADE, we have
`tan 22^circ = (AE)/(DE)`
`\implies 0.4040 = (AE)/15`
∴ AE = 15 × 0.4040
= 6.0600
= 6.06 m.
∴ CD = EB
= AB – AE
= 16.09 – 6.06
= 10.03 m
APPEARS IN
संबंधित प्रश्न
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45°, (ii) 60°. Find the height of the tower in each case.
The angles of elevation of the top of a tower from two points on the ground at distances a and b metres from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)` metre.
The top of a ladder reaches a pcint on the wall 5 m above the ground. If the foot of the ladder makes an angle of 30° with the ground, find the length of the ladder.
Find the angle of depression from the top of a 140m high pillar of a milestone on the ground at a distance of 200m from the foot of the pillar.
An observer, 1.5m tall, is 28.5m away from a tower 30m high. Determine the angle of elevation of the top of the tower from his eye.
The angle of elevation of a cloud from a point 60m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff. At a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff are 54° and 42° respectively. Find the height of the flagstaff. Give your answer correct to nearest metre.

