Advertisements
Advertisements
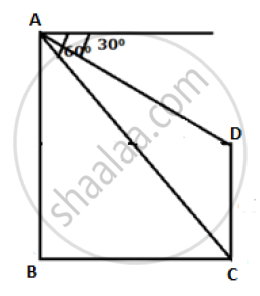
प्रश्न
Find AD.

उत्तर
In ΔABC,
∠ACD = ∠ABC + ∠BAC
And ∠ABC = ∠BAC ...(∵ AC = BC)
∴ ∠ABC = ∠BAC
= `48^circ/2`
= 24°
Now,
`(AD)/(AB) = sin 24^circ`
`=>` AD = 30 × 0.4067
= 12.20 m
APPEARS IN
संबंधित प्रश्न
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to 30o and 60o respectively. Find:
1) The horizontal distance between AB and CD.
2) The height of the lamp post.
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
The angle of elevation of the top of a tower is observed to be 60°. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45°. Find:
- the height of the tower,
- its horizontal distance from the points of observation.
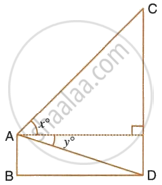
From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan `x^circ = 5/2` and the angle of depression of the foot D of the tower is y°, where tan `y^circ = 1/4`. Calculate the height CD of the tower in metres.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
Find the length of the shadow cast by a tree 60 m high when the sun's altitude is `30^circ`.
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
Vertical tower is 20m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
