Advertisements
Advertisements
प्रश्न
A man on the deck of a ship is 10 m above water level. He observes that the angle of elevation of the top of a cliff is 42° and the angle of depression of the base is 20°. Calculate the distance of the cliff from the ship and the height of the cliff.
उत्तर
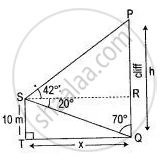
Let the height of the cliff be h meters and the distance of the cliff from the ship be x meters.
In right-angled ΔQRS,
∴ QR = ST = 10 m
TQ = RS = x m
∴ tan 70° = `"RS"/"QR"`
⇒ `2.747 = x/(10 m)`
∴ x = 27.47 m
Hence, the distance of the cliff from the ship = 27.47 m
Again in right angled ΔPRS,
∴ tan 42° = `"PR"/"RS"`
⇒ `0.9004 = "PR"/27.47`
⇒ PR = [ 0.9004 x 27.47 ] m
⇒ PR = 24.73 m
∴ PQ = PR + RQ
PQ = [ 24.73 + 10 ] m
PQ = 34.73 m
Hence the height of the cliff = 34.73 m.
APPEARS IN
संबंधित प्रश्न
A man observes the angle of elevation of the top of a building to be 30o. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60o. Find the height of the building correct to the nearest metre.
Prove the following identities:
tan2 A – sin2 A = tan2 A . sin2 A
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
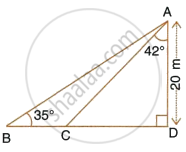
Calculate BC.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

A vertical pole is 90m high and the length of its shadow is `90sqrt(3)`. what is the angle of elevation of the sun ?
Of the two trees are on either side of a river, one of them is 50m high. From the top of this tree the angles of depression of the top and the foot of the other tree are 30° and 60° respectively. Find the width of the river and the height of the other tree.
A man in a boat rowing away from a lighthouse 180 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° and 30°. Find the speed of the boat.
A ladder rests against a wall at an angle a, to the horizontal. Its foot is pulled away from the wall through a distance 'a', so that it slides a distance 'b' down the wall making an angle β with the horizontal. Show that `"a"/"b" = (cosα - cosβ)/(sinβ - sinα).`
If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
