Advertisements
Advertisements
प्रश्न
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
उत्तर
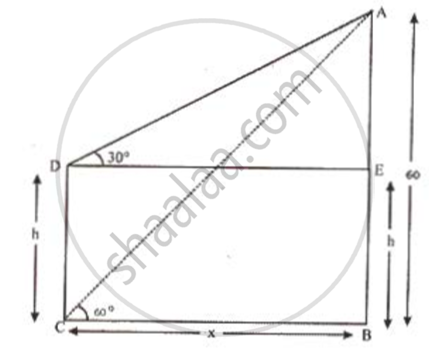
Let AB be the building. Then, AB = 60 m.
Let the height of the lamp post (CD) be h.
Let the distance between the building and the lamp post be x.
In ΔACB,
`tan60^circ = "AB"/"BC"`
∴ `sqrt(3) = 60/X`
∴ `X = 60/sqrt(3) = 20sqrt(3) = 20 × 1.732 = 34.64` ...(1)
Thus, the distance between the building and the lamp post is 34. 64 m
In ΔADE,
`tan30^circ = "AE"/"DE"`
∴ `1/sqrt(3) = (60 - h)/X`
∴ `X = sqrt(3)(60 - h)` ..(2)
From (1) and (2):
`sqrt(3)(60 - h) = 20sqrt(3)`
60 - h = 20
h = 40
APPEARS IN
संबंधित प्रश्न
In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to 30o and 60o respectively. Find:
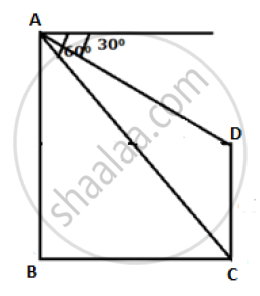
1) The horizontal distance between AB and CD.
2) The height of the lamp post.
Evaluate without using trigonometric tables.
`2((tan 35^@)/(cot 55^@))^2 + ((cot 55^@)/(tan 35^@)) - 3((sec 40^@)/(cosec 50^@))`
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
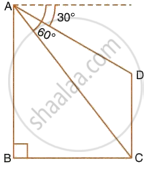
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
The length of the shadow of a pillar is `1/sqrt(3)` times the height of the pillar . find the angle of elevation of the sun .
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
From the top of a light house 96m high, the angles of depression of two ships in the river and at the same level as the base of the light house and on the same side of it, are α and β. If tan α = `1/4` and tan β = `1/7`, find the distance between the ships.
Two-person standing on the same side of a tower in a straight line with it measures the angle of elevation of the top of the tower as 25° and 50° respectively. If the height of the tower is 70 m find the distance between the two-person.
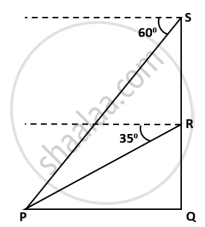
A drone camera is used to shoot an object P from two different positions R and S along the same vertical line QRS. The angle of depression of the object P from these two positions is 35° and 60° respectively as shown in the diagram. If the distance of the object P from point Q is 50 metres, then find the distance between R and S correct to the nearest meter.