Advertisements
Advertisements
Question
Find AD.
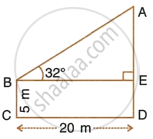
Solution
In ΔAEB,
= 12.50 m
∴ AD = AE + ED
= 12.50 + 5
= 17.50 m
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a tower, from a point on the ground and at a distance of 160 m from its foot, is found to be 60°. Find the height of the tower.
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
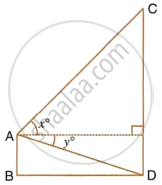
From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
An aeroplane, at an altitude of 250 m, observes the angles of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. If the boats are on the opposite sides of the aeroplane, find the width of the river. Write the answer correct to the nearest whole number.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
A man on the top of a tower observes that a car is moving directly at a uniform speed towards it. If it takes 720 seconds for the angle of depression to change from 30° to 45°, how soon will the car reach the observation tower?
The horizontal distance between towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60m, find the height of the first tower.
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.
