Advertisements
Advertisements
Question
A man on the top of a tower observes that a car is moving directly at a uniform speed towards it. If it takes 720 seconds for the angle of depression to change from 30° to 45°, how soon will the car reach the observation tower?
Solution
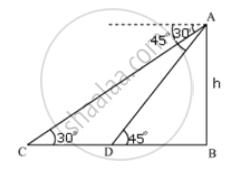
Let AB be the tower .
Initial position of car is C , which changes to D after 720 seconds.
In ΔADB
`"AB"/"DB" = tan45^circ`
`"AB"/"DB" = 1`
DB = AB
In ΔABC
`"AB"/"BC" = tan 30^circ`
`"AB"/"BD + DC" = 1/sqrt(3)`
`"AB"sqrt(3) = "BD + DC"`
`"AB"sqrt(3) = "AB + DC"`
`"DC" = "AB"sqrt(3) - "AB" = "AB"(sqrt(3) - 1)`
Time taken by car to travel DC distance (i.e `"AB"(sqrt(3) - 1`)) = 720 seconds
Time taken by car to travel DB distance (i.e. AB)
= `720/("AB"(sqrt(3) - 1)) xx "AB" = 720/((sqrt(3) - 1)) xx (sqrt(3) + 1)/(sqrt(3) + 1)`
= `(720(sqrt(3) + 1))/2 = 360(sqrt(3) + 1) = 360 xx 2.732 = 983.52`
Thus , the required time taken is 983.52 seconds = 984 seconds = 16 mins 24 secs.
APPEARS IN
RELATED QUESTIONS
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate, to the nearest metre, the distance of the buoy from the foot of the cliff.
Find the height of a tree when it is found that on walking away from it 20 m, in a horizontal line through its base, the elevation of its top changes from 60° to 30°.
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
A ladder rests against a tree on one side of a street. The foot of the ladder makes an angle of 50° with the ground. When the ladder is turned over to rest against another tree on the other side of the street it makes an angle of 40° with the ground. If the length of the ladder is 60m, find the width of the street.
A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of a diff is 45° and the angle of depression of the base is 30°. Find the distance of the diff from the ship and the height of the cliff.
The horizontal distance between towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60m, find the height of the first tower.
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
From an aeroplane vertically above a straight horizontal road, the angles of depression of two consecutive milestone on opposite sides of the aeroplane are observed to be α, and β. Show that the height in miles of aeroplane above the road is `(tanα tanβ)/(tanα + tanβ)`.
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

