Advertisements
Advertisements
प्रश्न
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
उत्तर
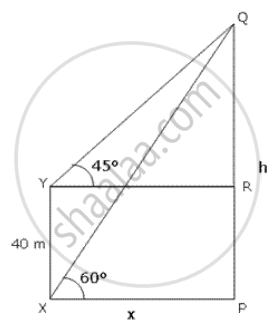
In the figure, PQ is the tower.
In ΔPQX,
∴ `"h"/"x" = tan60^circ = sqrt(3)`
⇒ h = `sqrt(3)`x ...(1)
In ΔQRY,
`("h" - 40)/"x" = tan 45^circ = 1`
⇒ h = 40 + x ...(2)
From (1) and (2),
`sqrt(3)`x = 40 + x
⇒ `(sqrt(3) - 1)"x" = 40`
⇒ `"x" = 40/(sqrt(3) - 1) = (40(sqrt(3) + 1))/((sqrt(3) - 1)(sqrt(3) + 1)) = 40/2(sqrt(3) + 1) = 20(sqrt(3) + 1)`
∴ `"h" = 40 + 20(sqrt(3) + 1) = 20sqrt(3) + 60 = 20(sqrt(3) + 3) = 20 xx 4.732 = 94.64`
Thus , the height of the tower PQ is 94.64 m.
Again, in ΔPQX,
∴ `"h"/"XQ" = sin60^circ = 1/sqrt(2)`
⇒ `"XQ" = sqrt(2)"h" = 1.414 xx 94.64 = 109.3`m
Thus , the distance XQ is 109.3m.
APPEARS IN
संबंधित प्रश्न
The angle of elevation from a point P of the top of a tower QR, 50 m high is 60o and that of the tower PT from a point Q is 30°. Find the height of the tower PT, correct to the nearest metre

An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
The angle of elevation of the top of an unfinished tower from a point at a distance of 80 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
A man stands 9 m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28° and the angle of depression of the bottom of the pole is 13°. Calculate the height of the pole.
The angle of elevation of the top of a tower is observed to be 60°. At a point, 30 m vertically above the first point of observation, the elevation is found to be 45°. Find:
- the height of the tower,
- its horizontal distance from the points of observation.
The horizontal distance between two trees of different heights is 100m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 150m, find the height of the first tree.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
Two men on either side of a temple 75 m high observed the angle of elevation of the top of the temple to be 30° and 60° respectively. Find the distance between the two men.
Vertical tower is 20m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
