Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of an unfinished tower from a point at a distance of 80 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
उत्तर
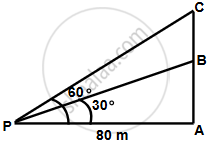
Let AB be the unfinished tower and C be the top of the tower when finished, Let P be a point 80 m from the foot A.
In ΔBAP,
`tan 30^circ = (AB)/(AP)`
`=> 1/sqrt(3) = (AB)/(80)`
`=> AB = 80/sqrt(3) = 46.19 m`
In ΔCAP,
`tan 60^circ = (AC)/(AP)`
`=> sqrt(3) = (AC)/(80)`
`=> AC = 80sqrt(3) = 138.56 m`
Therefore, the tower must be raised by (138.56 – 46.19) m = 92.37 m
APPEARS IN
संबंधित प्रश्न
Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
Find AD.

The angle of elevation of the top of a vertical cliff from a point 30 m away from the foot of the cliff is 60°. Find the height of the cliff.
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
A boy is standing on the ground and flying a kite with 100m of sting at an elevation of 30°. Another boy is standing on the roof of a 10m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
An aeroplane when 3,000 meters high passes vertically above another aeroplane at an instance when their angles of elevation at the same observation point are 60° and 45° respectively. How many meters higher is the one than the other?
The angles of elevation of the top of a tower from two points A and B at a distance of a and b respectively from the base and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)`.
A vertical tower standing on a horizontal plane is surmounted by a vertical flagstaff. At a point 100 m away from the foot of the tower, the angle of elevation of the top and bottom of the flagstaff are 54° and 42° respectively. Find the height of the flagstaff. Give your answer correct to nearest metre.

