Advertisements
Advertisements
प्रश्न
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
उत्तर
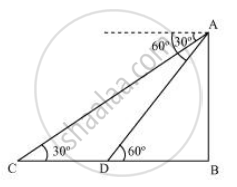
Let AB be the diff. Then , AB = 450 m
Initial position of boat is C , which changes to D after 3 minutes.
In ΔADB
`"AB"/"DB" = tan60^circ`
`450/"DB" = sqrt(3)`
`"DB" = 450/sqrt(3)`
In ΔABC
`"AB"/"BC" = tan30^circ`
`450/("BD + DC") = 1/sqrt(3)`
`450sqrt(3) = "BD + DC"`
`450sqrt(3) = 450/sqrt(3) + "DC"`
`"DC" = 450sqrt(3) - 450/(sqrt(3)) = 450(sqrt(3) - 1/sqrt(3))`
= `900/sqrt(3) = 900/sqrt(3) xx sqrt(3)/sqrt(3) = 300sqrt(3)`
Time taken by car to travel DC distance (`"i.e.,"300sqrt(3)`) = 3 minutes
Time taken by car to travel DB distance `("i.e". 450/sqrt(3))`
= `3/(300sqrt(3)) xx 450/sqrt(3) = 450/300 = 1.5`
Thus , the time it will take to reach the shore is 1 min 30 secs.
Speed of the boat = `"Distance"/"Time"`
= `(300sqrt(3))/3 = 100sqrt(3) = 100 xx 1.732 = 173.2` m/min
= `173.2/60` m/sec = 2.9 m/sec
APPEARS IN
संबंधित प्रश्न
A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68° with the ground. Find the height, upto which the ladder reaches.
Two climbers are at points A and B on a vertical cliff face. To an observer C, 40 m from the foot of the cliff, on the level ground, A is at an elevation of 48° and B of 57°. What is the distance between the climbers?
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
Two boats approaching a light house in mid sea from opposite directions observe the angle of elevation of the top of the light house as 30° and 45° respectively. If the distance between the two boats is 150m, find the height of the light house.
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° from two observing points 100 m apart to his right. Find the height from which he falls and the distance of the point where he falls on the ground from the nearest observation pcint.
A man standing on a cliff observes a ship at an angle of depression of the ship is 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
