Advertisements
Advertisements
प्रश्न
The angle of depression of a boat moving towards a diff is 30°. Three minutes later the angle of depression of the boat is 60°. Assuming that the boat is sailing at a uniform speed, determine the time it will take to reach the shore. Also, find the speed of the boat in m/second if the cliff is 450m high.
उत्तर
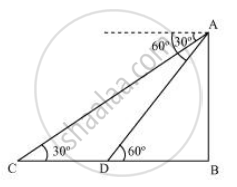
Let AB be the diff. Then , AB = 450 m
Initial position of boat is C , which changes to D after 3 minutes.
In ΔADB
`"AB"/"DB" = tan60^circ`
`450/"DB" = sqrt(3)`
`"DB" = 450/sqrt(3)`
In ΔABC
`"AB"/"BC" = tan30^circ`
`450/("BD + DC") = 1/sqrt(3)`
`450sqrt(3) = "BD + DC"`
`450sqrt(3) = 450/sqrt(3) + "DC"`
`"DC" = 450sqrt(3) - 450/(sqrt(3)) = 450(sqrt(3) - 1/sqrt(3))`
= `900/sqrt(3) = 900/sqrt(3) xx sqrt(3)/sqrt(3) = 300sqrt(3)`
Time taken by car to travel DC distance (`"i.e.,"300sqrt(3)`) = 3 minutes
Time taken by car to travel DB distance `("i.e". 450/sqrt(3))`
= `3/(300sqrt(3)) xx 450/sqrt(3) = 450/300 = 1.5`
Thus , the time it will take to reach the shore is 1 min 30 secs.
Speed of the boat = `"Distance"/"Time"`
= `(300sqrt(3))/3 = 100sqrt(3) = 100 xx 1.732 = 173.2` m/min
= `173.2/60` m/sec = 2.9 m/sec
APPEARS IN
संबंधित प्रश्न
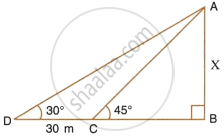
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
A man standing on the bank of a river observes that the angle of elevation of a tree on the opposite bank is 60°. When he moves 50 m away from the bank, he finds the angle of elevation to be 30°.
Calculate :
- the width of the river;
- the height of the tree.
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole is 60° and the angle of elevation of the top of the pole, as seen from the foot of the tower is 30°. Find:
- the height of the tower;
- the horizontal distance between the pole and the tower.
The top of a ladder reaches a pcint on the wall 5 m above the ground. If the foot of the ladder makes an angle of 30° with the ground, find the length of the ladder.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
The angle of elevation of a tower from a point 200 m from its base is θ, when `tan θ = 2/5`. The angle of elevation of this tower from a point 120m from its base is `Φ`. Calculate the height of tower and the value of `Φ`.
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
A man on the deck of a ship is 10 m above water level. He observes that the angle of elevation of the top of a cliff is 42° and the angle of depression of the base is 20°. Calculate the distance of the cliff from the ship and the height of the cliff.
