Advertisements
Advertisements
प्रश्न
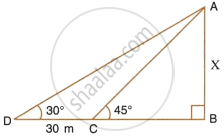
In the figure, given below, it is given that AB is perpandiculer to BD and is of length X metres. DC = 30 m, ∠ADB = 30° and ∠ACB = 45°. Without using tables, find X.
उत्तर
In ΔABC, we have
`tan 45^circ = (AB)/(CB) = X/(CB)` ...`[∵ tan theta = "Perpendicular"/"Base"]`
`1 = X/(CB)`
`\implies` CB = X ...(i)
Again in ΔADB, we have
`tan 30^circ = (AB)/(DB) = X/(DB)`
`\implies 1/sqrt(3) = X/(DB)`
∴ `DB = sqrt(3) xx X` ...(ii)
But DB = DC + CB
∴ `sqrt(3)X = 30 + X`
`\implies sqrt(3)X - X = 30`
`\implies X(sqrt(3) - 1) = 30`
`\implies X = 30/(sqrt(3) - 1)m`
∴ `X = (30(sqrt(3) + 1))/((sqrt(3) - 1)(sqrt(3) + 1))`
= `(30(sqrt(3) + 1))/(3 - 1)m`
= `(30(sqrt(3) + 1))/2`
= 15 (1.732 + 1) m.
= 15 × 2.732
= 40.98 m.
APPEARS IN
संबंधित प्रश्न
An aeroplane at an altitude of 1500 metres, finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships
An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
Prove the following identities:
sin4A – cos4A = 2sin2A – 1
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
A vertical pole is 90m high and the length of its shadow is `90sqrt(3)`. what is the angle of elevation of the sun ?
A kite tied to a string makes an angle of 60° with the ground. Find the perpendicular height of the kite if the length of its string is 250 m.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
If the angle of elevation of a cloud from a point h meters above a lake is a*and the angle of depression of its reflection in the lake is |i. Prove that the height of the cloud is `(h (tan β + tan α))/(tan β - tan α)`.
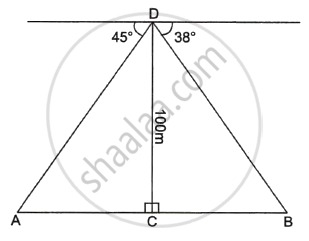
From the top of a tower 100 m high a man observes the angles of depression of two ships A and B, on opposite sides of the tower as 45° and 38° respectively. If the foot of the tower and the ships are in the same horizontal line find the distance between the two ships A and B to the nearest metre.
(Use Mathematical Tabels for this question)