Advertisements
Advertisements
प्रश्न
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
उत्तर
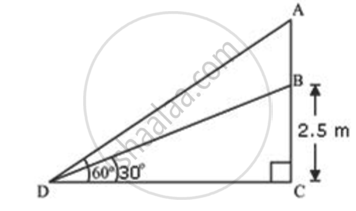
Let AB be the flagstaff, BC be the pole and D be the point on ground from where elevation angles are measured.
In ΔBCD
`"BC"/"CD" = tan 30^circ`
`"BC"/"CD" = 1/sqrt(3)`
`sqrt(3)"BC" = "CD"` ....(1)
In ΔACD
`("AB + BC")/"CD" = tan 60^circ`
`("AB + BC")/"CD" = sqrt(3)`
`"AB" + 2.5 = "CD"sqrt(3) = 3"BC"` [Using (1)]
`"AB" + 2.5 = 3 xx 2.5`
`"AB" + 2.5 = 7.5`
AB = 5
Thus , the height of the flagstaff is 5 m.
APPEARS IN
संबंधित प्रश्न
Prove the following identities:
sin4A – cos4A = 2sin2A – 1
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m and the string makes an angle 30° with the ground.
Calculate AB.

The radius of a circle is given as 15 cm and chord AB subtends an angle of 131° at the centre C of the circle. Using trigonometry, calculate:
- the length of AB;
- the distance of AB from the centre C.
A boy is standing on the ground and flying a kite with 100m of sting at an elevation of 30°. Another boy is standing on the roof of a 10m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
Two boats approaching a light house in mid sea from opposite directions observe the angle of elevation of the top of the light house as 30° and 45° respectively. If the distance between the two boats is 150m, find the height of the light house.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° from two observing points 100 m apart to his right. Find the height from which he falls and the distance of the point where he falls on the ground from the nearest observation pcint.
In figures, find the length CF.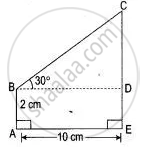
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

The angles of elevation of the top of a tower from two points A and B at a distance of a and b respectively from the base and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)`.
