Advertisements
Advertisements
Question
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

Solution
From the adjoining figure, in right-angled ΔBED,
`"DE"/"BE" = tan 45°`
DE = BE .....(1)
In right-angled ΔACD,
`"CD"/"AC" = tan 60°`
`60/"AC" = sqrt3`
AC = `60/sqrt3`
AC = `(60 xx sqrt3)/(sqrt3 xx sqrt3)`
AC = `(60 xx sqrt3)/3`
AC = `20sqrt3`
From (1), DE = BE = AC = `20 sqrt3`
Now, Hight of the tower = CD - DE
= `(60 - 20sqrt3)`m
= `20(3 - sqrt3)`m
= 20(3 − 1.73)
= 20(1.27)
= 25.4 m
APPEARS IN
RELATED QUESTIONS
At a particular time, when the sun’s altitude is 30°, the length of the shadow of a vertical tower is 45 m. Calculate:
- the height of the tower.
- the length of the shadow of the same tower, when the sun’s altitude is:
- 45°
- 60°
Find the height of a building, when it is found that on walking towards it 40 m in a horizontal line through its base the angular elevation of its top changes from 30° to 45°.
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
An aeroplane flying horizontally 1 km above the ground and going away from the observer is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°; find the uniform speed of the aeroplane in km per hour.
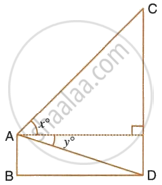
From a window A, 10 m above the ground the angle of elevation of the top C of a tower is x°, where tan `x^circ = 5/2` and the angle of depression of the foot D of the tower is y°, where tan `y^circ = 1/4`. Calculate the height CD of the tower in metres.
A 1.4m tall boy stands at a point 50m away from a tower and observes the angle of elevation of the top of the tower to be 60°. Find the height of the tower.
From a point 10 m above the ground , the angle of elevation of the top of a tower is α and the angle of depression is β . If tan α = `5/2` and tan β = `1/4` , calculate the height of the tower to the nearest metre .
An aeroplane when flying at a height of 4km from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplanes at that instant.
In figures, find the length CF.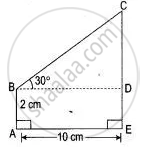
A man on the deck of a ship is 10 m above water level. He observes that the angle of elevation of the top of a cliff is 42° and the angle of depression of the base is 20°. Calculate the distance of the cliff from the ship and the height of the cliff.
