Advertisements
Advertisements
प्रश्न
An aeroplane at an altitude of 200 m observes the angles of depression of opposite points on the two banks of a river to be 45° and 60°. Find the width of the river.
उत्तर

Let AD be the height of the aeroplane and BC = x m be the width of the nver.
Given: AD=200m
In ΔABD
`"AD"/"BD" = tan45^circ`
⇒ `"AD"/"BD" = 1`
⇒ AD = BD
⇒ BD = 200m (∵ AD = 200m)
Now ,
In ΔACD
`"AC"/"CD" = tan60^circ`
⇒ `"AC"/"CD" = sqrt(3)`
⇒ `"CD" = "AC"/sqrt(3) = 200/sqrt(3)`
⇒ `"BC" = "BD" + "CD" = 200 + 200/sqrt(3) = 200 + 115.47`
⇒ `"BC" = 315.4` m
Thus, the width of the river is 315.4 m.
APPEARS IN
संबंधित प्रश्न
Two pillars of equal heights stand on either side of a roadway, which is 150 m wide. At a point in the roadway between the pillars the elevations of the tops of the pillars are 60° and 30°; find the height of the pillars and the position of the point.
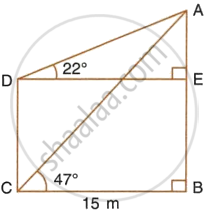
From the figure, given below, calculate the length of CD.
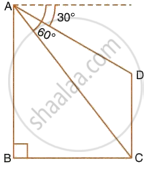
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships, on the same side of a light house in a horizontal line with its base, are 30° and 40° respectively. Find the distance between the two ships. Give your answer corrected to the nearest metre.
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
The angle of elevation of the top of an unfinished tower at a point 150 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
A man on the top of a tower observes a truck at an angle of depression ∝ where `∝ = 1/sqrt(5)` and sees that it is moving towards the base of the tower. Ten minutes later, the angle of depression of the truck is found to `β = sqrt(5)`. Assuming that the truck moves at a uniform speed, determine how much more ti me it will take to each the base of the tower?
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
The string of a kite is 150 m long and it makes an angle of 60° with the horizontal. Find the height of the kite from the ground.
The angle of elevation of a cloud from a point 200 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the cloud.
