Advertisements
Advertisements
प्रश्न
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
उत्तर
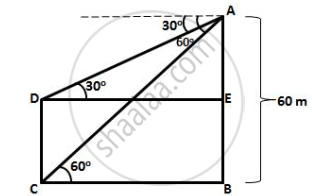
Let AB be the cliff and CD be the tower.
Here AB = 60 m, ∠ADE = 30° and ∠ACB = 60°
In ΔABC,
`(AB)/(BC) = tan 60^circ = sqrt(3)`
`=> BC = (60)/(sqrt(3))`
In ΔADE,
`(AE)/(DE) = tan 30^circ`
`=>` AE = DE tan 30°
= `60/(sqrt(3)) xx 1/sqrt(3)` ...[∵ DE = BC]
= 20 m
∴ CD = EB
= AB – AE
= (60 – 20)
= 40 m
Hence, height of the tower is 40 m.
APPEARS IN
संबंधित प्रश्न
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
Calculate BC.
From a point, 36 m above the surface of a lake, the angle of elevation of a bird is observed to be 30° and the angle of depression of its image in the water of the lake is observed to be 60°. Find the actual height of the bird above the surface of the lake.
A man observes the angle of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m, the angle of elevation changes to 60°. Find the height of the building correct to the nearest metre.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60° and the angle of depression of the bottom of the tower is 30°. Find:
- the height of the tower, if the height of the pole is 20 m;
- the height of the pole, if the height of the tower is 75 m.
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
A man on the top of a tower observes a truck at an angle of depression ∝ where `∝ = 1/sqrt(5)` and sees that it is moving towards the base of the tower. Ten minutes later, the angle of depression of the truck is found to `β = sqrt(5)`. Assuming that the truck moves at a uniform speed, determine how much more ti me it will take to each the base of the tower?
In triangle ABC, AB = 12 cm, LB = 58°, the perpendicular from A to BC meets it at D. The bisector of angle ABC meets AD at E. Calculate:
(i) The length of BD;
(ii) The length of ED.
Give your answers correct to one decimal place.

A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
