Advertisements
Advertisements
प्रश्न
A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
उत्तर
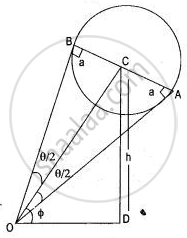
Let C be the centre of the balloon, O be the position of man's eye.
Let h be the height of the centre of the balloon.
Then, ∠AOB = θ
So, ∠BOC = ∠COA = `θ/2`
In ΔOAC,
sin θ/2 = `a/"OC"`
⇒ OC = a cosec `θ/2`
In ΔCOD,
`sin Φ = h/"OC"`
`⇒ h = OC sin Φ`
`⇒ h = a cosec θ/2 sin Φ`
`⇒ h = a sin Φ cosec θ/2`
APPEARS IN
संबंधित प्रश्न
Find AD.

The distance of the gate of a temple from its base is `sqrt(3)` times it height. Find the angle of elevation of the top of the temple.
An aeroplane takes off at angle of `30^circ` with the ground . Find the height of the aeroplane above the ground when it has travelled 386m without changing direction .
The horizontal distance between two trees of different heights is 100m. The angle of depression of the top of the first tree when seen from the top of the second tree is 45°. If the height of the second tree is 150m, find the height of the first tree.
The angles of depression of two cars on a straight road as observed from the top of a 42m high building are 60° and 75° respectively. Find the distance between the cars if they are on opposite sides of the building.
From the top of a 60m high building the angles of depression of the top and bottom of a lamp post are 30° and 60° respectively. Find the distance on the ground between the building and the lamp post and the difference in their heights.
The angle of elevation of a stationary cloud from a point 25m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. What is the height of the cloud above the lake-level?
From the top of a tower 60 m high, the angles of depression of the top and bottom of pole are observed to be 45° and 60° respectively. Find the height of the pole.

From the top of a lighthouse 100 m high the angles of depression of two ships on opposite sides of it are 48° and 36° respectively. Find the distance between the two ships to the nearest metre.
The angles of elevation of the top of a tower from two points A and B at a distance of a and b respectively from the base and in the same straight line with it are complementary. Prove that the height of the tower is `sqrt(ab)`.
