Advertisements
Advertisements
Question
Vertical tower is 20m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower?
Solution
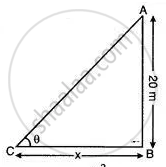
Given, cos θ = 0.53
Let the man is standing at a distance of 'x' m from the foot of the tower.
cos θ = `"BC"/"AC" = x/(sqrt(x^2 + 400))`
0.53 = `x/(sqrt(x^2 + 400))`
⇒ `(0.53)^2 = x^2/(sqrt(x^2 + 400))`
⇒ 0.2809 x2 + 112.36 = x2
⇒ x2 - 0.2809 x2 = 112.36
⇒ x2 = `(112.36)/(0.7191)`
⇒ x2 = 156.25
⇒ x = 12.5 metres
∴ The man is standing from the foot of the tower be 12.5 meter.
APPEARS IN
RELATED QUESTIONS
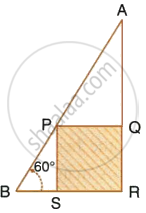
In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
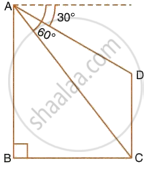
In the given figure, from the top of a building AB = 60 m hight, the angle of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
- the horizontal distance between AB and CD.
- the height of the lamp post.
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the top of the second is 30° and 24° respectively. Find the height of the two towers. Give your answers correct to 3 significant figures.

A man observes the angle of elevation of the top of the tower to be 45°. He walks towards it in a horizontal line through its base. On covering 20 m the angle of elevation changes to 60°. Find the height of the tower correct to 2 significant figures.
The height of an observation tower is 180m above sea level. A ship coming towards the tower is observed at an angle of depression of 30°. Calculate the distance of the boat from the foot of the observation tower.
A flagstaff stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. If the height of the pole is 2.5m. Find the height of the flagstaff.
The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
A vertical pole and a vertical tower are on the same level ground in such a way that from the top of the pole, the angle of elevation of the top of the tower is 60o and the angle of depression of the bottom of the tower is 30o. Find: the height of the pole, if the height of the tower is 75 m.
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.
An aeroplane at an altitude of 250 m observes the angle of depression of two Boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
