Advertisements
Advertisements
प्रश्न
A vertical tower stand on horizontel plane and is surmounted by a vertical flagstaff of height h metre. At a point on the plane, the angle of elevation of the bottom of the flagstaff is α and that of the top of flagstaff is β. Prove that the height of the tower is
`(h tan alpha)/(tan beta - tan alpha)`
उत्तर
Let height of tower AB = x
Height of flag staff CA = h.
Which makes the angles of elevation β and α at D.
In right ΔADB, we have
`tan alpha = (AB)/(DB) = x/(DB)`
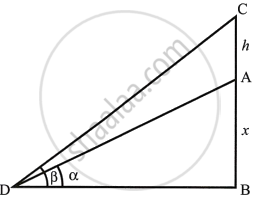
∴ `DB = x/(tan alpha)` ...(i)
And in right ΔCDB, we have
`tan beta = (CB)/(DB) = (h + x)/(DB)`
∴ `DB = (h + x)/(tan beta)` ...(ii)
From (i) and (ii)
`(h + x)/tan beta = x/tan alpha`
`\implies` h tan α + x tan α = x tan β
`\implies` h tan α = x tan β – x tan α
`\implies` h tan α = x (tan β – tan α)
∴ `x = (h tan alpha)/(tan beta - tan alpha)`
Hence required height of tower = `(h tan alpha)/(tan beta - tan alpha)`
APPEARS IN
संबंधित प्रश्न
The horizontal distance between two towers is 120 m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30° and 24° respectively.
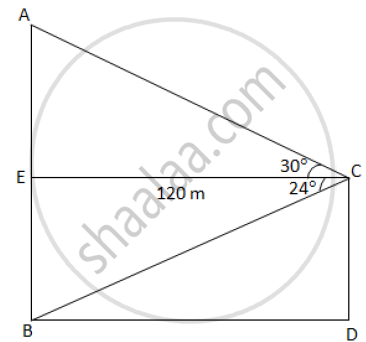
Find the height of the two towers. Give your answer correct to 3 significant figures
The height of a tree is `sqrt(3)` times the length of its shadow. Find the angle of elevation of the sun.
A boy, 1.6 m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45°, (ii) 60°. Find the height of the tower in each case.
The length of the shadow of a tower standing on level plane is found to be 2y metres longer when the sun’s altitude is 30° than when it was 45°. Prove that the height of the tower is `y(sqrt(3) + 1)` metres.
Find AD.

In the following diagram, AB is a floor-board; PQRS is a cubical box with each edge = 1 m and ∠B = 60°. Calculate the length of the board AB.
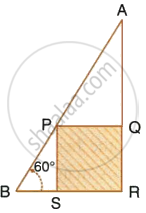
Calculate BC.
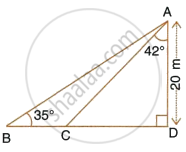
Calculate AB.

At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
The length of the shadow of a statue increases by 8m, when the latitude of the sun changes from 45° to 30°. Calculate the height of the tower.
