Advertisements
Advertisements
प्रश्न
A 10 m high pole is kept vertical by a steel wire. The wire is inclined at an angle of 40° with the horizontal ground. If the wire runs from the top of the pole to the point on the ground where Its other end is fixed, find the lenqth of the wire.
उत्तर
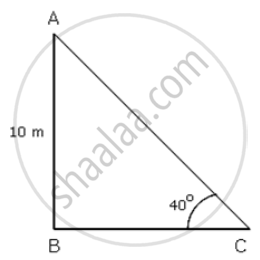
Let AB be the pole and AC be the wire which runs from the top of the pole to the point on the ground where its other end is fixed.
In ΔABC,
sin 40° = `"AB"/"AC"`
⇒ `0.6428 = 10/"AC"`
⇒ `"AC" = 10/0.6428 = 15.6`
Thus , the length of the wire is 15.6 m.
APPEARS IN
संबंधित प्रश्न
Two climbers are at points A and B on a vertical cliff face. To an observer C, 40 m from the foot of the cliff, on the level ground, A is at an elevation of 48° and B of 57°. What is the distance between the climbers?
From the top of a cliff, 60 metres high, the angles of depression of the top and bottom of a tower are observed to be 30° and 60°. Find the height of the tower.
The horizontal distance between two towers is 75 m and the angular depression of the top of the first tower as seen from the top of the second, which is 160 m high, is 45°. Find the height of the first tower.
At a point on level ground, the angle of elevation of a vertical tower is found to be such that its tangent is `5/12`. On walking 192 metres towards the tower, the tangent of the angle is found to be `3/4`. Find the height of the tower.
A vertical pole is 90m high and the length of its shadow is `90sqrt(3)`. what is the angle of elevation of the sun ?
The top of a palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9m from the foot of the tree. Find the original height of the palm tree.
The horizontal distance between towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60m, find the height of the first tower.
A man on the deck of a ship is 10 m above water level. He observes that the angle of elevation of the top of a cliff is 42° and the angle of depression of the base is 20°. Calculate the distance of the cliff from the ship and the height of the cliff.
A pole being broken by the wind the top struck the ground at an angle of 30° and at a distance of 8m from the foot of the pole. Find the whole height of the pole.
A round balloon of radius 'a' subtends an angle θ at the eye of the observer while the angle of elevation of its centre is Φ. Prove that the height of the centre of the balloon is a sin Φ cosec `θ/2`.
