Advertisements
Advertisements
प्रश्न
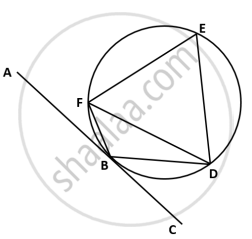
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
उत्तर
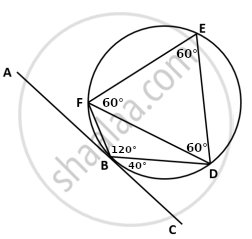
Given - In Diagram, ∆FED is an equilateral triangle, ∠CBD = 40°
To Find -
- ∠BFD,
- ∠FBD,
- ∠ABF
(a) ∠BFD = ∠CBD = 40° ....[Alternate segment theorem]
(b) ∠FBD is opposite to ∠FED.
So, It is a cyclic Quadrilateral. So, ∠FBD and ∠FED will be Supplementary to each other.
∴ ∠FBD + ∠FED = 180° ....[Cyclic Quadrilateral]
∠FBD + 60° = 180°
∠FBD = 180° - 60°
∠FBD = 120°
(c) AC is a line segment.
So, ∠ABF = 180° - (120° + 40°) ....[Line Segment]
∠ABF = 180° - 100°
∠ABF = 20°
APPEARS IN
संबंधित प्रश्न
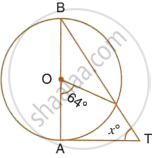
In the given figure, AB is the diameter of the circle, with centre O, and AT is the tangent. Calculate the numerical value of x.
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
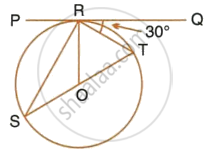
Given O is the centre of the circle and angle TRQ = 30°.
ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
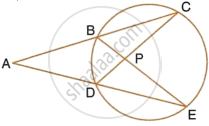
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
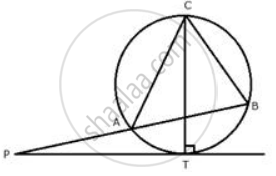
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

