Advertisements
Advertisements
प्रश्न
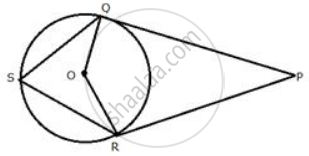
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

उत्तर
∠QRP = ∠OSR = y ...(Angles in the alternate segment)
But OS = OR ...(Radii of the same circle)
∴ ∠ORS = ∠OSR = y°
∴ OQ = OR ...(Radii of the same circle)
∴ ∠OQR = ∠ORQ = 90° – y° ...(i) (Since OR ⊥ PT)
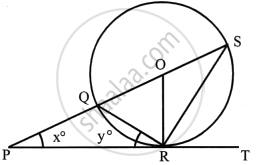
But in ΔPQR,
Ext. ∠OQR = x° + y° ...(i)
From (i) and (ii)
x° + y° = 90° – y°
`=>` x° + 2y° = 90°
APPEARS IN
संबंधित प्रश्न
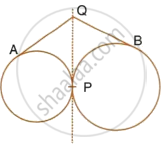
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

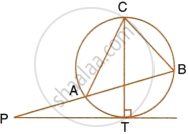
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

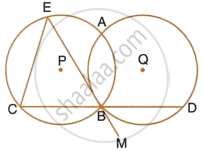
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ QSR
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.
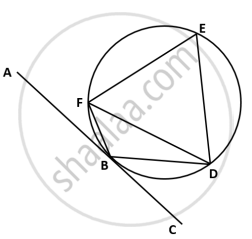
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
