Advertisements
Advertisements
प्रश्न
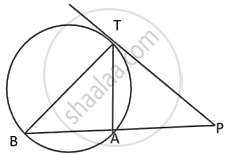
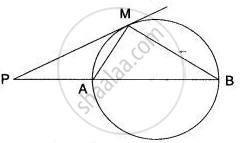
In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.
उत्तर
AC = BC
⇒ ∠CBA = ∠CAB
⇒ ∠CAB = 50°
∴ ∠ACB = 180° - (50° + 50°) = 80°
Now, ∠BAT = ∠BCA ....(Angles are in alternate segments)
⇒ ∠BAT = 80°.
APPEARS IN
संबंधित प्रश्न
In the following figure; If AB = AC then prove that BQ = CQ.

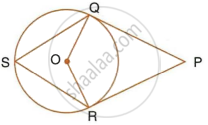
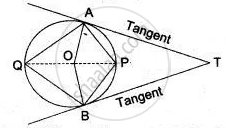
In the following figure, PQ and PR are tangents to the circle, with centre O. If `∠`QPR = 60°, calculate:
- ∠QOR,
- ∠OQR,
- ∠QSR.
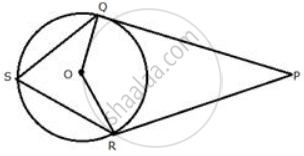
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ OQR
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB
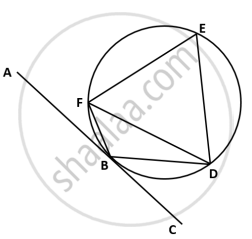
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.