Advertisements
Advertisements
प्रश्न
Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
उत्तर
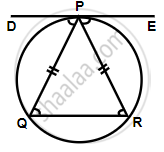
DE is the tangent to the circle at P.
DE || QR ...(Given)
∠EPR = ∠PRQ ...(Alternate angles are equal)
∠DPQ = ∠PQR (Alternate angles are equal) ...(i)
Let ∠DPQ = x and ∠EPR = y
Since the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment
∴ ∠DPQ = ∠PRQ ...(ii) (DE is tangent and PQ is chord)
From (i) and (ii)
∠PQR = ∠PRQ
`=>` PQ = PR
Hence, triangle PQR is an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
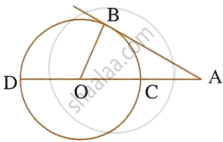
In the given figure, O is the center of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
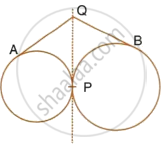
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
In the following figure; If AB = AC then prove that BQ = CQ.

In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
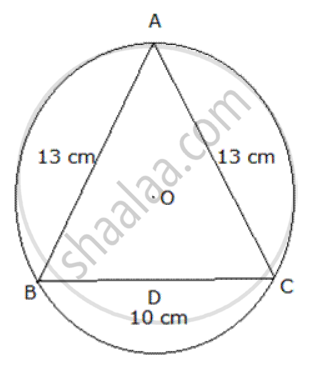
In figure , ABC is an isosceles triangle inscribed in a circle with centre O such that AB = AC = 13 cm and BC = 10 cm .Find the radius of the circle.
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
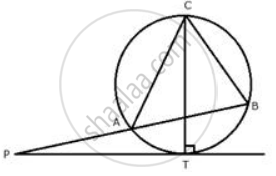
In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.
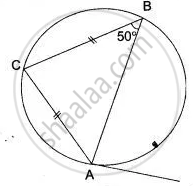
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

