Advertisements
Advertisements
प्रश्न
AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
उत्तर
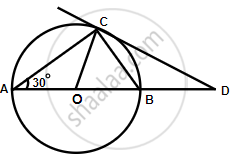
Join OC,
∠BCD = ∠BAC = 30° ...(Angles in alternate segment)
Arc BC subtends ∠DOC at the centre of the circle and ∠BAC at the remaining part of the circle.
∴ ∠BOC = 2∠BAC = 2 × 30° = 60°
Now in ΔOCD,
∠BOC or ∠DOC = 60°
∠OCD = 90° ...(OC ⊥ CD)
∴ ∠DCO + ∠ODC = 90°
`=>` 60° + ∠ODC = 90°
`=>` ∠ODC = 90° – 60° = 30°
Now in ΔBCD,
∵ ∠ODC or ∠BDC = ∠BCD = 30°
∴ BC = BD
APPEARS IN
संबंधित प्रश्न
The radius of a circle is 8 cm. calculate the length of a tangent draw to this circle from a point at a distance of 10 cm from its centre.
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

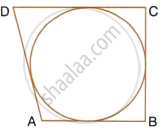
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

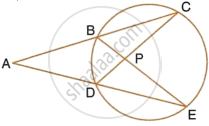
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
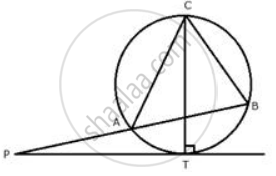
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

