Advertisements
Advertisements
प्रश्न
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

उत्तर
i. AB is a diameter.
∴ ∠ACB = 90°
The angle in a semicircle is the right angle.
∴ In ΔACB,
∠A + ∠C + ∠B = 180°
34° + 90° + ∠B = 180°
∠B = 180° – (34° + 90°)
∠B = 180° – 124°
∠B = 56°
ii. Now,
CQ is tangent.
∴ ∠QCB = ∠CAB ...(Alternate segment angle)
∴ ∠QCB = 34°
And ∠CBQ = 180° – ∠CBA
∠CBQ = 180° – 56° = 124°
∴ ∠CQA = 180° – (∠QCB + ∠CBQ)
∠CQA = 180° – (34° + 124°)
∠CQA = 180° – 158° = 22°.
APPEARS IN
संबंधित प्रश्न
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
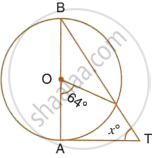
In the given figure, AB is the diameter of the circle, with centre O, and AT is the tangent. Calculate the numerical value of x.
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

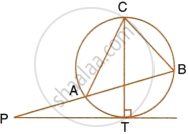
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.
In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

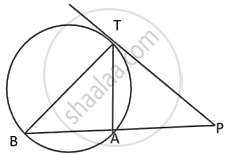
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.