Advertisements
Advertisements
प्रश्न
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
उत्तर
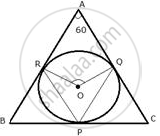
The incircle touches the sides of the triangle ABC and OP ⊥ BC, OQ ⊥ AC, OR ⊥ AB
i. In quadrilateral AROQ,
∠ORA = 90°, ∠OQA = 90°, ∠A = 60°
∠QOR = 360° – (90° + 90° + 60°)
∠QOR = 360° – 240°
∠QOR = 120°
ii. Now arc RQ subtends ∠QOR at the centre and ∠QPR at the remaining part of the circle.
∴ `∠QPR = 1/2 ∠QOR`
`=> ∠QPR = 1/2 xx 120^circ`
`=>` ∠QPR = 60°
APPEARS IN
संबंधित प्रश्न
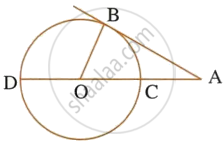
In the given figure, O is the center of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
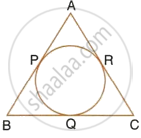
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
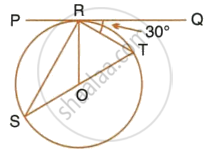
Given O is the centre of the circle and angle TRQ = 30°.
Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
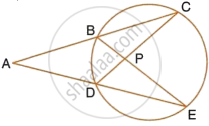
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ QSR
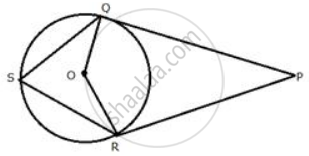
In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°
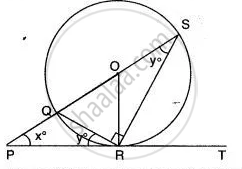
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB
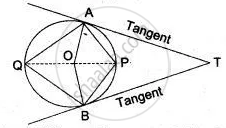
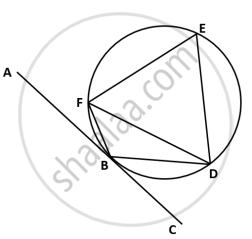
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
