Advertisements
Advertisements
प्रश्न
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
उत्तर
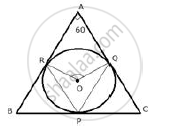
The incircle touches the sides of the triangle ABC and
OP ⊥ BC,OQ ⊥ AC,OR ⊥ AB
i) Now arc RQ subtends`∠`QOR at the centre and `∠`QPR at the remaining part of the circle.
∴ `∠`QPR = `1/2` `∠` QOR
⇒ `∠`QPR = `1/2 xx120°`
⇒ `∠` QPR = 60°
APPEARS IN
संबंधित प्रश्न
The radius of a circle is 8 cm. calculate the length of a tangent draw to this circle from a point at a distance of 10 cm from its centre.
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

In the following figure; If AB = AC then prove that BQ = CQ.

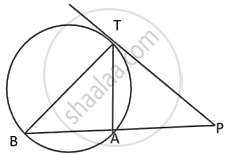
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

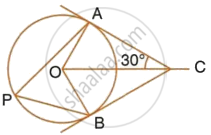
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°, find:
- ∠BCO
- ∠AOB
- ∠APB
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
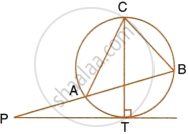
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.