Advertisements
Advertisements
प्रश्न
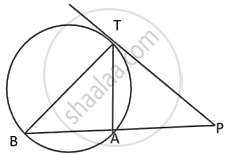
In the given figure PT is a tangent to the circle. Chord BA produced meets the tangent PT at P.
Given PT = 20 cm and PA = 16 cm.
- Prove ΔPTB ~ ΔPAT
- Find the length of AB.
उत्तर
a. In ΔPTB and ΔPAT,
∠ PTA = ∠PBT ...(Alternate segment theorem)
∠TPA = ∠BPT ...(Common ∠)
∴ ΔPTB ~ ΔPAT ...(AA axiom)
b. PA × PB = PT2
`\implies` 16(16 + AB) = 400
`\implies` 16 + AB = 25
`\implies` AB = 9 cm
APPEARS IN
संबंधित प्रश्न
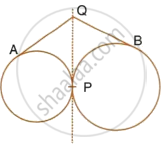
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
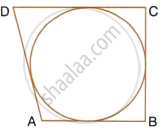
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
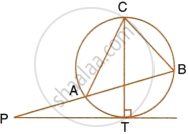
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

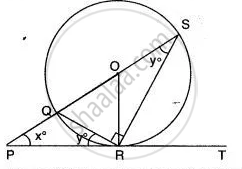
In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

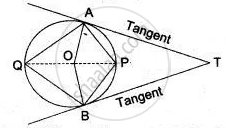
In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB
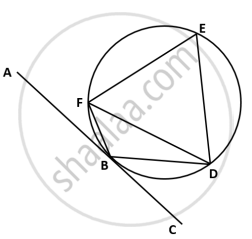
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
