Advertisements
Advertisements
प्रश्न
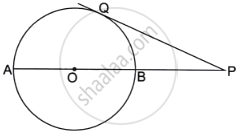
In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

उत्तर
i. PAQ is a tangent and AB is the chord.
∠QAB = ∠ADB = 30° ...(Angles in the alternate segment)
ii. OA = OD ...(Radii of the same circle)
∴ ∠OAD = ∠ODA = 30°
But, OA ⊥ PQ
∴ ∠PAD = ∠OAP – ∠OAD
= 90° – 30°
= 60°
iii. BD is the diameter.
∴ ∠BCD = 90° ...(Angle in a semi-circle)
Now in ΔBCD,
∠CDB + ∠CBD + ∠BCD = 180°
`=>` ∠CDB + 60° + 90° = 180°
`=>` ∠CDB = 180° – (60° + 90°)
`=>` ∠CDB = 180° – 150° = 30°
APPEARS IN
संबंधित प्रश्न
The radius of a circle is 8 cm. calculate the length of a tangent draw to this circle from a point at a distance of 10 cm from its centre.
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

In the following figure; If AB = AC then prove that BQ = CQ.

In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
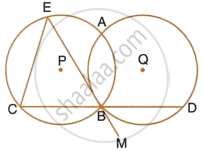
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ: