Advertisements
Advertisements
Question
In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

Solution
i. PAQ is a tangent and AB is the chord.
∠QAB = ∠ADB = 30° ...(Angles in the alternate segment)
ii. OA = OD ...(Radii of the same circle)
∴ ∠OAD = ∠ODA = 30°
But, OA ⊥ PQ
∴ ∠PAD = ∠OAP – ∠OAD
= 90° – 30°
= 60°
iii. BD is the diameter.
∴ ∠BCD = 90° ...(Angle in a semi-circle)
Now in ΔBCD,
∠CDB + ∠CBD + ∠BCD = 180°
`=>` ∠CDB + 60° + 90° = 180°
`=>` ∠CDB = 180° – (60° + 90°)
`=>` ∠CDB = 180° – 150° = 30°
APPEARS IN
RELATED QUESTIONS
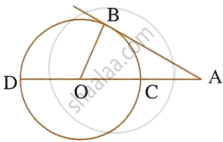
In the given figure, O is the center of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
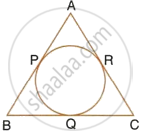
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
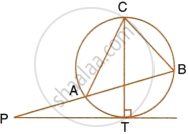
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
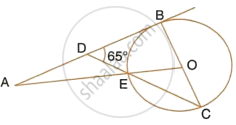
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
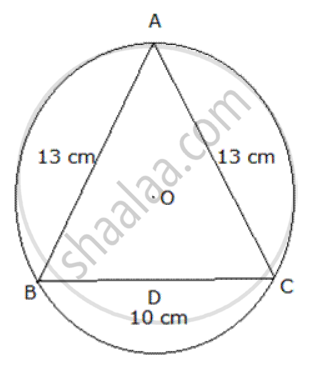
In figure , ABC is an isosceles triangle inscribed in a circle with centre O such that AB = AC = 13 cm and BC = 10 cm .Find the radius of the circle.
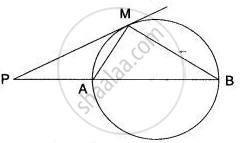
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2
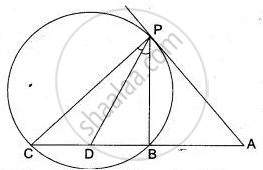
In Fig. AP is a tangent to the circle at P, ABC is secant and PD is the bisector of ∠BPC. Prove that ∠BPD = `1/2` (∠ABP - ∠APB).
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
