Advertisements
Advertisements
Question
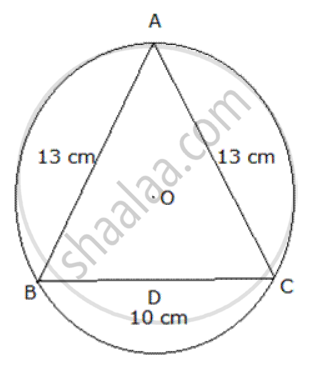
In figure , ABC is an isosceles triangle inscribed in a circle with centre O such that AB = AC = 13 cm and BC = 10 cm .Find the radius of the circle.
Solution
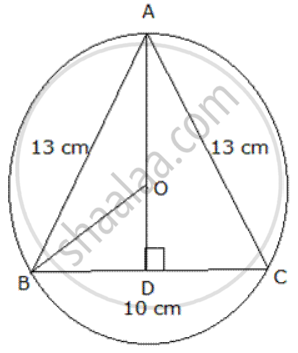
Since ABC is an isosceles triangle, AOO is the perpendicular bisector of BC.
In triangle ADC, by Pythagoras theorem we have
AD2 = AC2 - DC2 = 132 - 52 = 169 - 25 = 144
⇒ AD = 12 cm ⇒ AO + OD = 12 ⇒ AO = 12 - x ...(Assuming OD = x cm)
Again in triangle OBD,
BO2 = BD2 + OD2 = 25 + x2 ..(As BD = 5 cm)
⇒ (12 - x)2 = 25 + x2 ..(As AO = BO = radius)
⇒ 144 + x2 - 24 x = 25 + x2
⇒ -24 x = 25 - 144 = - 119
⇒ x = 4.96 cm
⇒ AO = 12 - 4. 96 = 7 .04 cm
APPEARS IN
RELATED QUESTIONS
From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
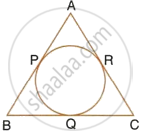
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
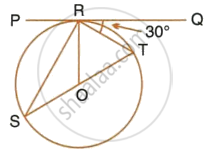
Given O is the centre of the circle and angle TRQ = 30°.
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

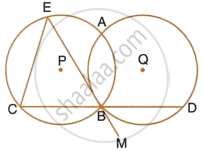
Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
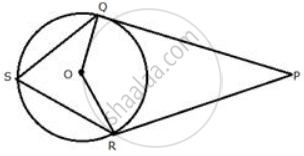
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ OQR
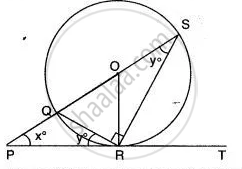
In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°
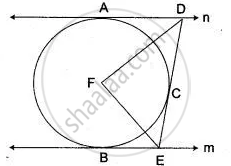
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ: