Advertisements
Advertisements
Question
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ OQR
Solution
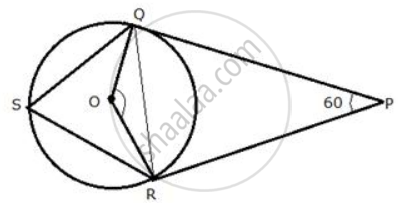
Join QR.
In Δ QOR,
OQ = QR (Radii of the same circle)
∴ ∠ OQR = ∠ QRO .....(i)
but , ∠OQR + ∠QRO + ∠QOR = 180°
∠OQR + ∠ QRO +120° = 180°
∠OQR + ∠QRO = 60°
from (i)
2 ∠OQR = 60°
∠ OQR = 30°
APPEARS IN
RELATED QUESTIONS
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

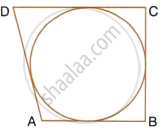
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
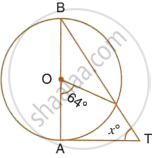
In the given figure, AB is the diameter of the circle, with centre O, and AT is the tangent. Calculate the numerical value of x.
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
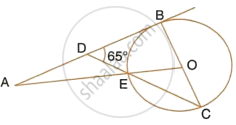
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
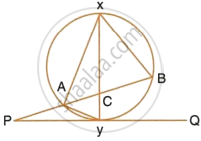
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ QSR
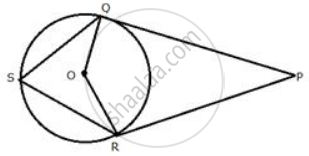
In Fig. AP is a tangent to the circle at P, ABC is secant and PD is the bisector of ∠BPC. Prove that ∠BPD = `1/2` (∠ABP - ∠APB).