Advertisements
Advertisements
Question
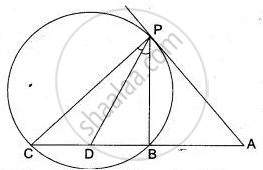
In Fig. AP is a tangent to the circle at P, ABC is secant and PD is the bisector of ∠BPC. Prove that ∠BPD = `1/2` (∠ABP - ∠APB).
Solution
Since ∠APB and ∠BCP are angles in the alternate segment of chord PB.
∴ ∠APB = ∠BCP ...(i)
Since PD is the bisector of ∠BPC.
∴ ∠CPB = 2 ∠BPD ...(ii)
In ΔPCB, side CB has been produced to A, forming exterior angle ∠ABP.
∴ ∠ABP = ∠BCP + ∠CPB
⇒ ∠ABP = ∠APB + 2 ∠BPD ....(Using (i) and (ii))
⇒ 2 ∠BPD = ∠ABP - ∠APB
⇒ ∠BPD = `1/2`(∠ABP - ∠APB)
Hence proved.
APPEARS IN
RELATED QUESTIONS
In the following figure; If AB = AC then prove that BQ = CQ.

In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
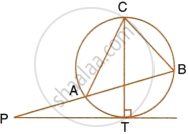
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
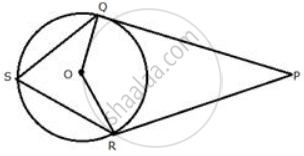
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ OQR
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.
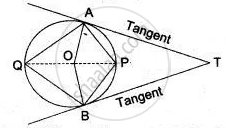
In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB