Advertisements
Advertisements
Question
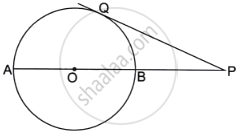
In the following figure; If AB = AC then prove that BQ = CQ.

Solution
Since, from A, AP and AR are the tangents to the circle
Therefore, AP = AR
Similarly, we can prove that
BP = BQ and CR = CQ
Adding,
AP + BP + CQ = AR + BQ + CR
(AP + BP) + CQ = (AR + CR) + BQ
AB + CQ = AC + BQ
But AB = AC
Therefore, CQ = BQ or BQ = CQ
APPEARS IN
RELATED QUESTIONS
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
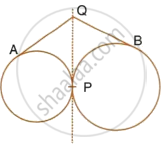
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
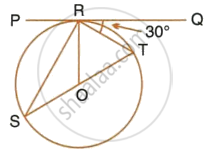
Given O is the centre of the circle and angle TRQ = 30°.
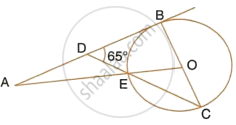
In the adjoining figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
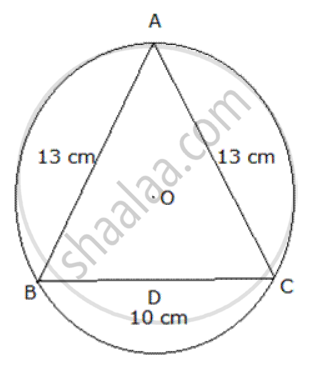
In figure , ABC is an isosceles triangle inscribed in a circle with centre O such that AB = AC = 13 cm and BC = 10 cm .Find the radius of the circle.
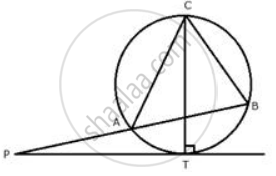
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
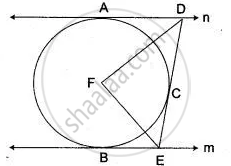
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ: