Advertisements
Advertisements
Question
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

Solution
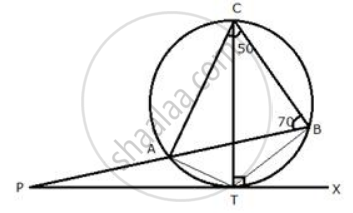
Join AT and BT.
∠ CBA = 70°
∴ ∠ABT = ∠CBT - ∠CBA = 90° - 70° = 20°
Now , ∠ ACT = ∠ABT = 20° (Angles the same segment of the circle)
∴ ∠TCB = ∠ACB - ∠ACT = 50° - 20° = 30°
But , ∠TCB = ∠TAB (Angles in the same segment of the circle)
But , ∠TCB or ∠BAT = 30°
APPEARS IN
RELATED QUESTIONS
The radius of a circle is 8 cm. calculate the length of a tangent draw to this circle from a point at a distance of 10 cm from its centre.
From the given figure, prove that : AP + BQ + CR = BP + CQ + AR.
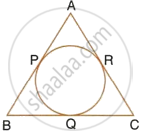
Also show that : AP + BQ + CR = `1/2` × Perimeter of ΔABC.
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
In quadrilateral ABCD; angles D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm, Find the radius of the circle.
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

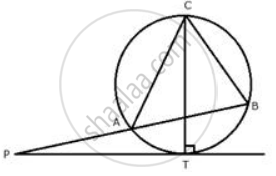
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
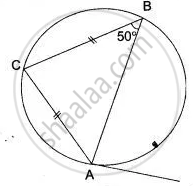
In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.
A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.
In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

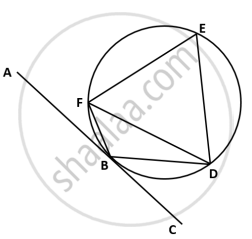
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
