Advertisements
Advertisements
Question
In quadrilateral ABCD; angles D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm, Find the radius of the circle.
Solution
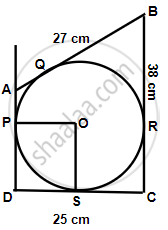
BQ and BR are the tangents from B to the circle.
Therefore, BR = BQ = 27 cm.
Also RC = (38 − 27) = 11 cm
Since CR and CS are the tangents from C to the circle
Therefore, CS = CR = 11 cm
So, DS = (25 − 11) = 14 cm
Now DS and DP are the tangents to the circle
Therefore, DS = DP
Now, `∠`PDS = 90° ...(Given)
And OP ⊥ AD, OS ⊥ DC
Therefore, radius = DS = 14 cm
APPEARS IN
RELATED QUESTIONS
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
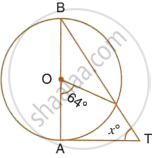
In the given figure, AB is the diameter of the circle, with centre O, and AT is the tangent. Calculate the numerical value of x.
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
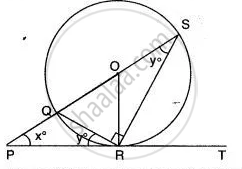
In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
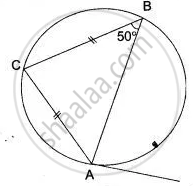
In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.
A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.
