Advertisements
Advertisements
Question
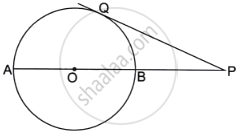
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

Solution
i. PA is the tangent and AB is a chord
∴ ∠PAB = ∠C ...(i) (Angles in the alternate segment)
AD is the bisector of ∠BAC
∴ ∠1 = ∠2 ...(ii)
In ΔADC,
Ext. ∠ADP = ∠C + ∠1
`=>` Ext ∠ADP = ∠PAB + ∠2 = ∠PAD
Therefore, ΔPAD is an isosceles triangle.
ii. In ΔABC,
Ext. ∠PBA = ∠C + ∠BAC
∴ ∠BAC = ∠PBA – ∠C
`=>` ∠1 + ∠2 = ∠PBA – ∠PAB ...(From (i) part)
`=>` 2∠1 = ∠PBA – ∠PAB
`=> ∠1 = 1/2 (∠PBA - ∠PAB)`
`=> ∠CAD = 1/2 (∠PBA - ∠PAB)`
APPEARS IN
RELATED QUESTIONS
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

In the following figure; If AB = AC then prove that BQ = CQ.

In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
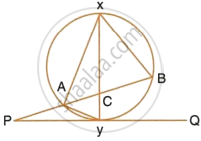
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

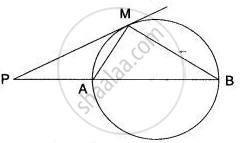
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2
A circle touches the sides of a quadrilateral ABCD at P, Q, R, S respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
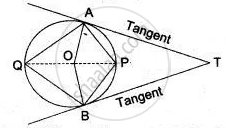
In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB
The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ: