Advertisements
Advertisements
Question
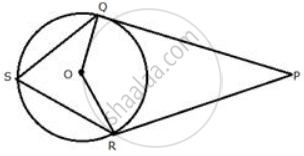
Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
Solution
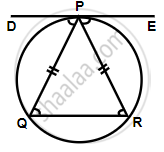
DE is the tangent to the circle at P.
DE || QR ...(Given)
∠EPR = ∠PRQ ...(Alternate angles are equal)
∠DPQ = ∠PQR (Alternate angles are equal) ...(i)
Let ∠DPQ = x and ∠EPR = y
Since the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment
∴ ∠DPQ = ∠PRQ ...(ii) (DE is tangent and PQ is chord)
From (i) and (ii)
∠PQR = ∠PRQ
`=>` PQ = PR
Hence, triangle PQR is an isosceles triangle.
APPEARS IN
RELATED QUESTIONS
The radius of a circle is 8 cm. calculate the length of a tangent draw to this circle from a point at a distance of 10 cm from its centre.
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
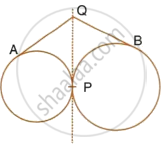
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
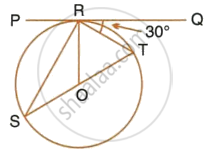
Given O is the centre of the circle and angle TRQ = 30°.
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ OQR
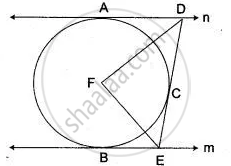
In Fig. l and m are two parallel tangents at A and B. The tangent at C makes an intercept DE between n and m. Prove that ∠ DFE = 90°
In Fig. AT is a tangent to the circle. If m∠ABC = 50°, AC = BC, Find ∠BAT.