Advertisements
Advertisements
प्रश्न
Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
उत्तर
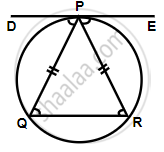
DE is the tangent to the circle at P.
DE || QR ...(Given)
∠EPR = ∠PRQ ...(Alternate angles are equal)
∠DPQ = ∠PQR (Alternate angles are equal) ...(i)
Let ∠DPQ = x and ∠EPR = y
Since the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment
∴ ∠DPQ = ∠PRQ ...(ii) (DE is tangent and PQ is chord)
From (i) and (ii)
∠PQR = ∠PRQ
`=>` PQ = PR
Hence, triangle PQR is an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
In the given figure, O is the center of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
- ∠QOR
- ∠QPR;
given that ∠A = 60°.
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT

A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.
The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ: