Advertisements
Advertisements
प्रश्न
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

उत्तर
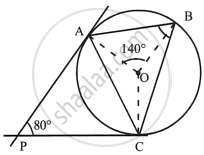
Join OC.
Therefore, PA and PC are the tangents
∴ OA ⊥ PA and OC ⊥ PC
In quadrilateral APCO,
∠APC + ∠AOC = 180°
∠BOC = 360° – (∠AOB + ∠AOC)
∠BOC = 360° – (140° + 100°)
∠BOC = 360° – 240° = 120°
Now, arc BC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle.
∴
APPEARS IN
संबंधित प्रश्न
If the sides of a quadrilateral ABCD touch a circle, prove that : AB + CD = BC + AD.

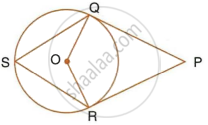
In the following figure, PQ and PR are tangents to the circle, with centre O. If
- ∠QOR,
- ∠OQR,
- ∠QSR.
In quadrilateral ABCD; angles D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm, Find the radius of the circle.
In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

If PQ is a tangent to the circle at R; calculate:
- ∠PRS,
- ∠ROT.
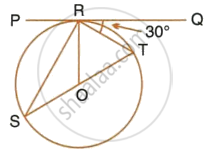
Given O is the centre of the circle and angle TRQ = 30°.
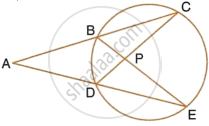
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
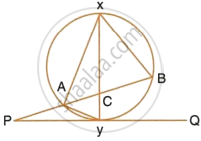
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
In Fig. AP is a tangent to the circle at P, ABC is secant and PD is the bisector of ∠BPC. Prove that ∠BPD =
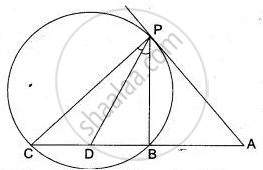
A, B, and C are three points on a circle. The tangent at C meets BN produced at T. Given that ∠ ATC = 36° and ∠ ACT = 48°, calculate the angle subtended by AB at the center of the circle.
In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

