Advertisements
Advertisements
प्रश्न
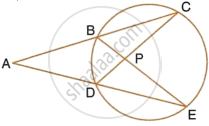
In the given figure, AC = AE. Show that:
- CP = EP
- BP = DP
उत्तर
In ΔADC and ΔABE,
∠ACD = ∠AEB ...(Angles in the same segment)
AC = AE ...(Given)
∠A = ∠A ...(Common)
∴ ΔADC ≅ ΔABE ...(ASA postulate)
`=>` AB = AD
But AC = AE
∴ AC – AB = AE – AD
`=>` BC = DE
In ΔBPC and ΔDPE
∠C = ∠E ...(Angles in the same segment)
BC = DE
∠CBP = ∠CDE ...(Angles in the same segment)
∴ ΔBPC ≅ ΔDPE ...(ASA Postulate)
`=>` BP = DP and CP = PE ...(C.P.C.T.)
APPEARS IN
संबंधित प्रश्न
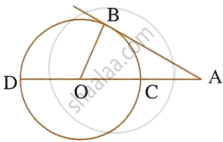
In the given figure, O is the center of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
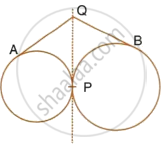
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at points P, Q and R respectively. Calculate:
i)`∠`QPR .
In the given figure, O is the centre of the circumcircle ABC. Tangents at A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.

In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

Circles with centres P and Q intersect at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circle are congruent; show that CE = BD.
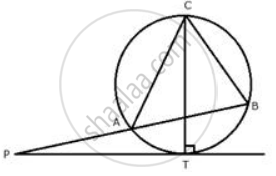
PT is a tangent to the circle at T. If ∠ ABC = 70° and ∠ ACB = 50° ; calculate : ∠ APT
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

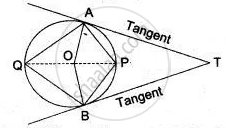
In the adjoining diagram TA and TB are tangents, O is the centre. If ∠ PAT = 35° and ∠ PBT = 40°.
Calculate:
(i) ∠ AQP, (ii) ∠ BQP
(iii) ∠ AQB, (iv) ∠ APB
(v) ∠ AOB, (vi) ∠ ATB