Advertisements
Advertisements
प्रश्न
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
उत्तर
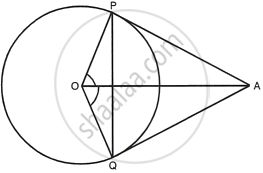
In quadrilateral OPAQ,
∠OPA = ∠OQA = 90°
(∵ OP ⊥ PA and OQ ⊥ QA)
∴ `∠`POQ + `∠`PAQ + 90° + 90° = 360°
`=>` ∠POQ + ∠PAQ = 360° – 180° = 180° ...(i)
In triangle OPQ,
OP = OQ ...(Radii of the same circle)
∴ OPQ = ∠OQP
But ∠POQ + ∠OPQ + ∠OQP = 180°
`=>` ∠POQ + ∠OPQ + ∠OPQ = 180°
`=>` ∠POQ + 2∠OPQ = 180° ...(ii)
From (i) and (ii)
∠POQ + ∠PAQ = ∠POQ + 2∠OPQ
`=>` ∠PAQ = 2∠OPQ
APPEARS IN
संबंधित प्रश्न
The radius of a circle is 8 cm. calculate the length of a tangent draw to this circle from a point at a distance of 10 cm from its centre.
Two circle touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
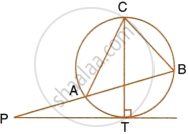
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
In the following figure, PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB = 30° and ∠CBD = 60°, calculate:
- ∠QAB,
- ∠PAD,
- ∠CDB.

Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
In the figure; PA is a tangent to the circle, PBC is secant and AD bisects angle BAC. Show that triangle PAD is an isosceles triangle. Also, show that:
`∠CAD = 1/2 (∠PBA - ∠PAB)`

TA and TB are tangents to a circle with centre O from an external point T. OT intersects the circle at point P. Prove that AP bisects the angle TAB.
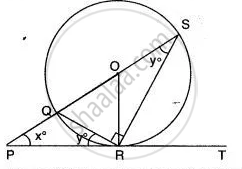
In the given figure, PT touches a circle with centre O at R. Diameter SQ when produced to meet the tangent PT at P. If ∠SPR = x° and ∠QRP = y°; Show that x° + 2y° = 90°
In Fig. AP is a tangent to the circle at P, ABC is secant and PD is the bisector of ∠BPC. Prove that ∠BPD = `1/2` (∠ABP - ∠APB).
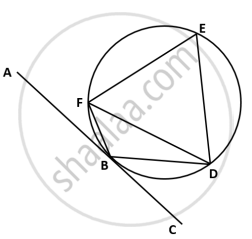
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
