Advertisements
Advertisements
Question
Tangents AP and AQ are drawn to a circle, with centre O, from an exterior point A. Prove that : ∠PAQ = 2∠OPQ
Solution
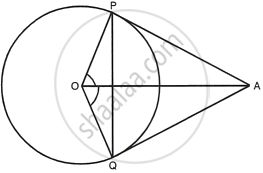
In quadrilateral OPAQ,
∠OPA = ∠OQA = 90°
(∵ OP ⊥ PA and OQ ⊥ QA)
∴ `∠`POQ + `∠`PAQ + 90° + 90° = 360°
`=>` ∠POQ + ∠PAQ = 360° – 180° = 180° ...(i)
In triangle OPQ,
OP = OQ ...(Radii of the same circle)
∴ OPQ = ∠OQP
But ∠POQ + ∠OPQ + ∠OQP = 180°
`=>` ∠POQ + ∠OPQ + ∠OPQ = 180°
`=>` ∠POQ + 2∠OPQ = 180° ...(ii)
From (i) and (ii)
∠POQ + ∠PAQ = ∠POQ + 2∠OPQ
`=>` ∠PAQ = 2∠OPQ
APPEARS IN
RELATED QUESTIONS
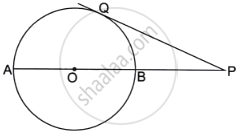
In the given figure, O is the center of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, calculate the radius of the circle.
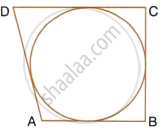
If the sides of a parallelogram touch a circle in following figure, prove that the parallelogram is a rhombus.
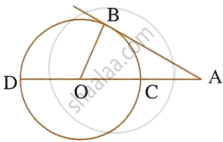
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
In quadrilateral ABCD; angles D = 90°, BC = 38 cm and DC = 25 cm. A circle is inscribed in this quadrilateral which touches AB at point Q such that QB = 27 cm, Find the radius of the circle.
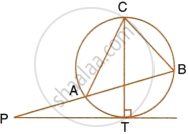
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate:
- ∠CBT
- ∠BAT
- ∠APT
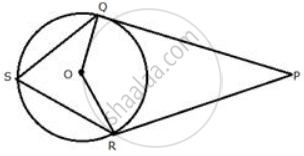
In the following figure, PQ and PR are tangents to the circle, with centre O. If ∠ QPR = 60° , calculate:
∠ OQR
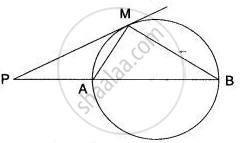
In the figure, PM is a tangent to the circle and PA = AM. Prove that:
(i) Δ PMB is isosceles
(ii) PA x PB = MB2
In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

The figure shows a circle of radius 9 cm with 0 as the centre. The diameter AB produced meets the tangent PQ at P. If PA = 24 cm, find the length of tangent PQ: