Advertisements
Advertisements
Question
In the joining figure shown XAY is a tangent. If ∠ BDA = 44°, ∠ BXA = 36°.
Calculate: (i) ∠ BAX, (ii) ∠ DAY, (iii) ∠ DAB, (iv) ∠ BCD.

Solution
(i) ∠ BAX = ∠ BDA = 44° ...(Angles in the alternate segment)
(ii) ∠ ABD = ∠ BXA + ∠ BAX
∠ ABD = 36° + 44° = 80° ....(Ext. angle of a triangle = sum of internal opposite angles)
∴ ∠ DAY = ∠ ABD = 80° ...(Angles in the alternate segment)
(iii) ∠ DAB = 180° - (∠ BAX + ∠ DAY)
∠ DAB = 180° - (44° + 80°) = 56°
(v) ∠ BCD = 180° - ∠ DAB
∠ BCD = 180° - 56° = 124° ...(Opposite ∠ s of a cyclic quadrilateral are supplementary)
APPEARS IN
RELATED QUESTIONS
From a point P outside a circle, with centre O, tangents PA and PB are drawn. Prove that:
∠AOP = ∠BOP
In the following figure, PQ and PR are tangents to the circle, with centre O. If `∠`QPR = 60°, calculate:
- ∠QOR,
- ∠OQR,
- ∠QSR.
In the given figure, PT touches the circle with centre O at point R. Diameter SQ is produced to meet the tangent TR at P. Given ∠SPR = x° and ∠QRP = y°;
Prove that:
- ∠ORS = y°
- write an expression connecting x and y.

AB is the diameter and AC is a chord of a circle with centre O such that angle BAC = 30°. The tangent to the circle at C intersects AB produced in D. show that BC = BD.
Tangent at P to the circumcircle of triangle PQR is drawn. If the tangent is parallel to side, QR show that ΔPQR is isosceles.
ABC is a right triangle with angle B = 90°, A circle with BC as diameter meets hypotenuse AC at point D. Prove that: AC × AD = AB2
In the given figure, XY is the diameter of the circle and PQ is a tangent to the circle at Y.
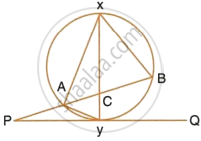
If ∠AXB = 50° and ∠ABX = 70°, find ∠BAY and ∠APY.
In the Figure, PT is a tangent to a circle. If m(∠BTA) = 45° and m(∠PTB) = 70°. Find m(∠ABT).

In the given figure, AB is the diameter. The tangent at C meets AB produced at Q. If ∠CAB = 34°, find:
- ∠CBA
- ∠CQB

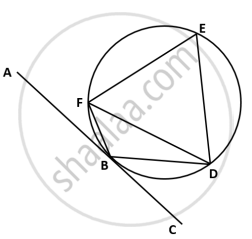
In the given figure, AC is a tangent to circle at point B. ∆EFD is an equilateral triangle and ∠CBD = 40°. Find:
- ∠BFD
- ∠FBD
- ∠ABF
